Trim of Ship and Methods To Calculate

This document explains how to determine a ship’s trim the difference between aft and forward drafts – for design work, new construction, and operational decisions.

It defines the main terms, lists the hydrostatic data required, presents the common calculation methods (small-change linear approach and full nonlinear equilibrium), and gives a practical, repeatable procedure for routine use.

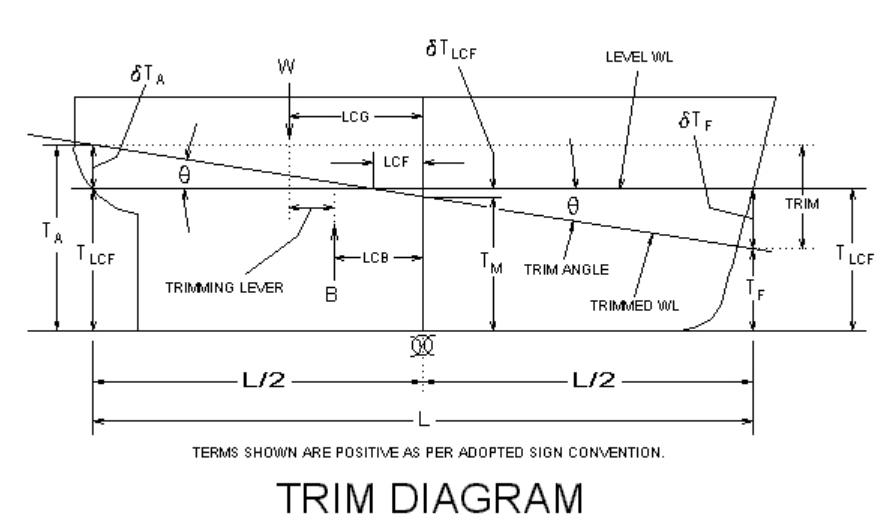
It also covers units and sign conventions, iterative approaches for large changes, and verification steps to ensure results are accurate and safe.

Fundamental Concepts

Trim definition

• Trim is the longitudinal difference between the aft draft and the forward draft. Trim by stern is positive when the stern is deeper than the bow.

Drafts and mean draft

• Forward draft $T_f$ and aft draft $T_a$.

• Mean draft $T_m=(T_f+T_a)\mathrm{/}2$.

• Centre of Buoyancy B: centroid of the immersed volume; moves with draft and trim.

• Longitudinal Centre of Flotation LCF: effective pivot point for small trimming changes; the centroid of the waterplane area.

Centers and reference points

• Centre of Gravity G: longitudinal location of the ship’s weight.

Hydrostatic coefficients

• Displacement Δ: vessel weight expressed as mass or tonnes.

• Moment to Change Trim MCT: moment required to change trim by a unit amount (commonly t·m per cm).

• Tons Per Centimeter Immersion TPC: change in displacement per centimeter change of mean draft (t/cm).

• Trimming arm: longitudinal distance from LCF to a reference point such as the forward or aft perpendicular or to draft measurement points.

Hydrostatic Data and Units

Required hydrostatic particulars

• Displacement as a function of draft.

• MCT values at relevant drafts (per cm or per inch).

• TPC at the operating draft.

• LCF and LCB positions as functions of draft and, if available, trim.

• Waterplane area moment of inertia or trimming arms if MCT must be calculated from geometry.

Distances and geometry

• Length between perpendiculars or other reference length used for trim geometry.

• Distances from LCF to forward and aft draft points or to the perpendiculars.

Units and sign conventions

• Use consistent units: metric tonnes for weight, metres for distances, and t·m for moments when using MCT in t·m/cm.

• Positive trim means stern-down (Ta − Tf > 0).

• Positive trimming moment produces stern-down rotation about the LCF.

Calculation Methods

Small-change linear method using MCT

1. Compute the trimming moment TM about the LCF from weight shifts or additions:

• For a weight Wmoved from x_1to x_2(measured from LCF): $\text{TM}=W\times (x_2-x_1)$ (tonne·m).

2. Obtain MCT per cm at the current mean draft.

    3. Compute trim change in cm: $\mathrm{\Delta }\text{trim}=\text{TM}\mathrm{/}{\text{MCT}}_{1\text{cm}}$.

    4. Apply the trim about the LCF to get draft changes at bow and stern using trimming arms or distances to perpendiculars.

    5. If weight was added or removed, compute uniform sinkage using TPC and add it to both drafts.

Large-change nonlinear equilibrium method

• For large weight changes or when immersion of hull sections changes significantly, hydrostatic properties vary with draft and trim. Solve the two equilibrium conditions numerically: buoyant force equals ship weight, and longitudinal moments balance (sum of moments about a datum equals zero). Iterate on mean sinkage and trim until both conditions are satisfied.

Alternative approximations

              Use the relation between MCT and longitudinal metacentric height GMl for rough estimates: MCT_1m≈Δ×GM_l/L. Prefer hydrostatic table values over approximations.

Step-by-Step Procedure

Operational workflow

1. Gather inputs: current T_f, T_a, T_m, displacement Δ, LCF, MCT, TPC, distances to FP and AP, and the list of weight changes or shifts with positions.
2. Compute trimming moment TM about the LCF for each weight action and sum them to get the net TM. Use sign convention that positive TM produces stern-down.
3. Estimate trim change using MCT: $\mathrm{\Delta }\text{trim}=\text{TM}\mathrm{/}{\text{MCT}}_{1\text{cm}}$.
4. Compute sinkage if net weight change ΔΔ exists: sinkage (cm)=ΔΔ/TPC.
5. Apply changes about LCF:

• Change at stern $\mathrm{\Delta }{T}_a=\text{sinkage}+\mathrm{\Delta }\text{trim}\times (d_{\text{LCF→AP}}\mathrm{/}{L}_{\text{ref}})$.

• Change at bow $\mathrm{\Delta }{T}_f=\text{sinkage}-\mathrm{\Delta }\text{trim}\times (d_{\text{LCF→FP}}\mathrm{/}{L}_{\text{ref}})$.

• Update drafts and mean draft: $T_m^{\text{new}}=T_m^{\text{old}}+(\mathrm{\Delta }{T}_a+\mathrm{\Delta }{T}_f)\mathrm{/}2$.

   6. Iterate: if hydrostatic values (MCT, LCF, TPC) change beyond tolerance, interpolate new values from hydrostatic tables at the updated mean draft and repeat steps 2–5 until convergence (e.g., change < 0.1 cm).

Worked numeric example

• Given: T_f=6.20 m, T_a=7.00 m, so T_m=6.60 m and initial trim = 0.80 m (80 cm). Δ = 12,500 t. LCF is 5.0 m aft of midships; LBP = 100 m; distances to AP and FP from midships are 50 m and − 50 m respectively, so LCF→AP = 45 m and LCF→FP = −55 m. A 20 t weight is moved 30 m aft (from 10 m forward of midships to 20 m aft). MCT1cm = 250 t·m/cm.

• Compute TM: convert positions to LCF datum and multiply by 20 t to get TM (tonne·m).

• Compute Δtrim: $\mathrm{\Delta }\text{trim (cm)}=\text{TM}\mathrm{/}250$.

• Compute sinkage if weight added or removed and update drafts using trimming arms as above.

• Iterate if hydrostatic values change significantly.

Practical Implementation and Verification

Iterative considerations

• Hydrostatic coefficients vary with draft and trim; for moderate to large changes, update MCT, LCF, TPC, and LCB by interpolation from the hydrostatic tables each iteration.

• Stop iterating when changes in trim and mean draft between cycles fall below a chosen tolerance.

Accuracy and safety checks

• Verify that the new displacement from hydrostatic tables matches the ship’s weight within tolerance.

• Confirm moment equilibrium by comparing the longitudinal moment of weights about the chosen datum with the buoyancy moment (Δ × LCB).

• Correct for water density differences (fresh vs salt water) because displacement and TPC depend on density.

Implementation tips for spreadsheets or software

• Inputs: initial drafts, list of weight moves/additions, and hydrostatic table arrays keyed by draft with Δ, TPC, MCT, LCF, and LCB.

• Use linear interpolation between hydrostatic table entries or higher-order interpolation for greater accuracy.

• Structure an iteration loop that recomputes TM about the updated LCF, fetches updated hydrostatic coefficients, recalculates trim and sinkage, and repeats until convergence.

• Provide warnings when predicted drafts approach structural or operational limits.

Best practices

• Prefer measured hydrostatic data, model test results, or validated software outputs for MCT and LCF rather than geometric approximations.

• Keep a clear record of all weight movements and the positions used in calculations.

• Use conservative rounding and include safety margins when planning operations near limits.

Summary

Calculating trim reliably combines a clear understanding of hydrostatic properties with consistent sign and unit conventions and an iterative approach when changes are large.

For routine, small adjustments, the MCT-based linear method is efficient and accurate. For large changes or when hull immersion changes significantly, solve the full buoyancy and moment equilibrium numerically using updated hydrostatic data.

Always validate results against the ship’s hydrostatic tables, correct for water density, and document the steps taken.